Syntaxe abstraite UML pour B

Syntaxe abstraite UML pour B

Ce méta-modèle est disponible au format ecore : BMethod.ecore
N'hésitez pas à me contacter pour toute suggestion (Akram.Idani@imag.fr)
All rights reserved ©

Pour citer ce méta-modèle

1  Méta-modèle B

Le méta-modèle que nous proposons pour B donne une vue structurelle de haut niveau reprenant les notions définies au niveau de la syntaxe B. Nous nous en servons ici pour donner une vision globale des dépendances entre les différentes constructions du langage B.

Dans un premier temps, nous procéderons à la spécification du méta-modèle correspondant à une machine abstraite B (Fig. 4), ensuite nous proposerons un méta-modèle exprimant le typage en B (Fig. 9), et finalement, nous terminons par le méta-modèle relatif aux compositions et aux raffinements (Fig. 10). Ces méta-modèles seront étayés par une description des principales méta-classes ainsi que des principales contraintes d'utilisation (ou règles de bonne formation). Pour des raisons de clarté, nous décrirons ces contraintes d'utilisation d'une manière informelle.

1.1  Spécification de machines abstraites

Une machine abstraite, représentée par la méta-classe BMachine, est constituée de plusieurs clauses permettant de spécifier les parties statiques et dynamiques du système. La partie statique correspond aux déclarations d'ensembles, de constantes et de variables et une caractérisation de ces données en termes de propriétés des constantes (clause PROPERTIES) et d'invariants. Nous ne faisons pas cette distinction par clauses au niveau du méta-modèle relatif aux machines abstraites car nous ne trouvons pas de contrepartie en UML. Il est, certes, possible de proposer une extension d'UML pour la prise en compte d'une telle structuration. Cependant, nous limitons notre étude, à ce niveau, aux constructions de base d'UML en vue de produire des diagrammes simples et compréhensibles. C'est pourquoi nous n'évoquerons au niveau de notre méta-modèle que les constructions en B susceptibles d'être transformées en UML. Nous définissons la méta-classe abstraite BData pour spécifier toutes les données déclarées au niveau d'une machine B (ensembles abstraits, constantes et variables). Quant à la partie dynamique, elle est spécifiée par les deux méta-classes BOperation et BInitialisation qui permettent de représenter respectivement les opérations et l'initialisation d'une spécification B. Notons que le méta-modèle complet relatif à la spécification des machines abstraites et présenté au niveau de la Fig. 4. Toutefois, nous allons en présenter certains morceaux ci-dessous pour illustrer les différentes définitions.


BMachine (Fig. 1).  Représente une machine abstraite B. Elle est composée d'un ensemble de données B (méta-classe BData), d'un ensemble d'opérations (méta-classe BOperation), d'un ensemble d'invariants1 (méta-classe BInvariant), d'un ensemble de paramètres (méta-classe BMachineParam), et finalement de l'initialisation (méta-classe BInitialisation). Nous la définissons pour constituer la spécification d'un module B.
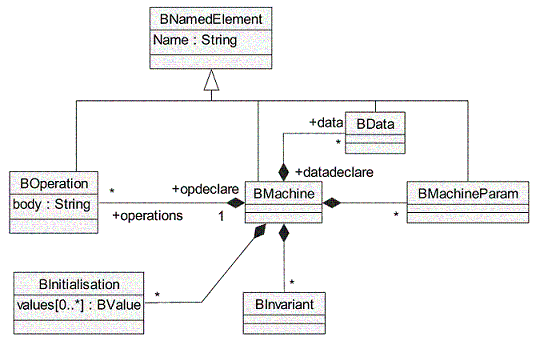BMachine.png
Figure 1: Composition de la méta-classe BMachine
BOperation (Fig. 2).  Spécifie les opérations d'une machine abstraite B. Chaque opération est composée de paramètres (BOpParameter) et de substitutions (BSubstitution). Chaque accès d'une BOperation à une BData est qualifié par un type d'accès (attribut Kind). Cette notion d'accès sera traitée plus finement dans le chapitre . Néanmoins, nous notons que l'accès d'une BOperation O à une BData D en précondition correspond au fait que D apparait dans le corps d'une instance de BPrecondition (voir Fig. 2) liée à une substitution (Méta-classe BSubstitution) de O. Dans le cadre d'un développement B construit par composition, il peut y avoir des appels entre opérations (cas d'une inclusion entre machines (Fig. 10)). Ces appels ainsi que les règles de visibilité associées seront spécifiés dans la section 1.3. Au niveau de la syntaxe B nous distinguons plusieurs contraintes d'utilisation des opérations telles que :

    (i) Les paramètres formels d'une opération doivent être deux à deux distincts ;
    (ii) Les paramètres d'entrée d'une opération doivent être typés dans le prédicat pré-condition. Ce qui signifie que si une opération est paramétrée alors une pré-condition lui est associée ;
    (iii) Les paramètres sont distincts des variables et des constantes de la BMachine.
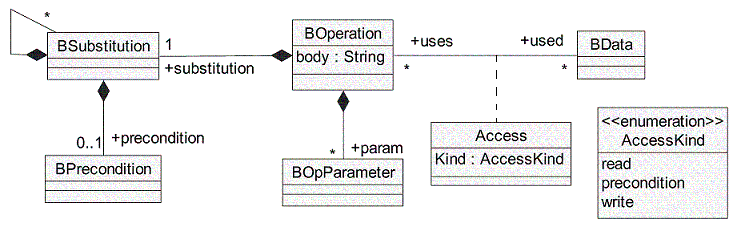BOperationMeta.png
Figure 2: Dépendances et composition de la méta-classe BOperation
BPrecondition.  Cette méta-classe ne spécifie pas uniquement la précondition associée à une substitution préconditionnée. En effet, elle prend en compte des prédicats associées à d'autres substitutions. Nous disons que P est une instance de la méta-classe BPrecondition dans les cas suivants :
IF P THEN S ELSE T END
ASSERT P THEN S END
PRE P THEN S END
SELECT P THEN S END
ANY z WHERE P THEN S END

BData (Fig. 3).    Définit les variables, constantes et ensembles abstraits déclarés et spécifiés au niveau des clauses SETS, CONSTANTS et VARIABLES. Les contraintes d'utilisation de la méta-classe BData sont principalement associées aux spécialisations BConstant et BSet. Il s'agit précisément de restreindre l'accès des opérations à un accès en précondition ou en lecture quand il s'agit d'un accès à un BSet ou à une BConstant.

    (iv) Si une instance de la classe associative Access est créée entre une opération quelconque (instance de BOperation) et une instance de BSet ou de BConstant, alors son attribut Kind vaut "read" ou "precondition".
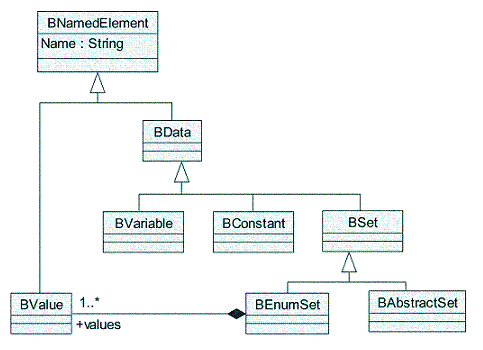BDataMeta.png
Figure 3: Spécialisations de la méta-classe BData


BNamedElement.  Représente tous les éléments du modèle qui doivent être nommés au niveau de la spécification : machines, opérations, données B et paramètres.


BInitialisation.  Définit l'initialisation des variables de la machine abstraite. Une instance de BInitialisation correspond à une substitution généralisée qui permet d'associer une (ou plusieurs) valeur(s) (BValue) de départ pour une variable (BVariable) de la machine. Bien qu'il soit possible d'utiliser dans l'initialisation toutes les sortes d'instructions, la manière usuelle d'initialiser les variables consiste à utiliser des substitutions devient égal ":=". Nous parlons alors d'initialisation déterministe. Dans ce cas, la valeur initiale de la variable est identifiée par l'attribut values[0..*] : BValue de la méta-classe BInitialisation. Le caractère multi-valué de l'attribut values permet de considérer le cas d'une initialisation non-déterministe (e.g. substitution devient appartient ": ∈ " ou devient tel que ":()") et telle que les valeurs initiales possibles d'une variable sont explicitement définies (e.g. une variable v initialisée par v : ∈ E où E est un ensemble énuméré). Lorsque ces valeurs ne sont par définies explicitement au niveau de la spécification, l'attribut values n'est pas instancié vu que c'est un attribut optionnel.


BSet.  Spécifie les ensembles déclarés au niveau de la clause SETS d'une machine abstraite. Nous distinguons deux spécialisations de la méta-classe BSet : la méta-classe BEnumSet et la méta-classe BAbstractSet (Fig. 3). Ces sous-classes de BSet caractérisent respectivement les ensembles énumérés (BEnumSet) et les ensembles abstraits (BAbstractSet).


BValue.  Représente l'ensemble des valeurs pré-définies par le langage B (par exemple les valeur TRUE et FALSE de l'ensemble BOOL des booléens) ou définies au niveau d'une machine abstraite par énumération.


BPredicate.  Classe abstraite représentant les prédicats associés aux invariants et aux préconditions des substitutions. Étant donné que nous nous intéressons à la structure des machines B nous mettons en évidence les données et valeurs qui composent un prédicat.


La Fig. 4 illustre le méta-modèle que nous proposons en vue de représenter la spécification des machines abstraites en B. Notons que nous ne détaillons pas les notions de BSubstitution et de BExpression étant donné que nous n'allons pas nous en servir au niveau de notre travail. Nous mettons en évidence à ce niveau les constituants d'une machine abstraite et les dépendances entre ces constituants sans nous attacher aux détails ni à la manière dont on peut former les substitutions généralisées. L'accès d'une BOperation o à une BData d peut être affiné au moyen d'un lien entre la(les) BSubstitution(s) qui composent l'opération o et la donnée d si ces BSubstitutions utilisent d. Pour faciliter l'expression des schémas de transformation de B vers UML que nous présenterons dans le chapitre suivant nous nous contentons du lien Access entre BOperations et BDatas.
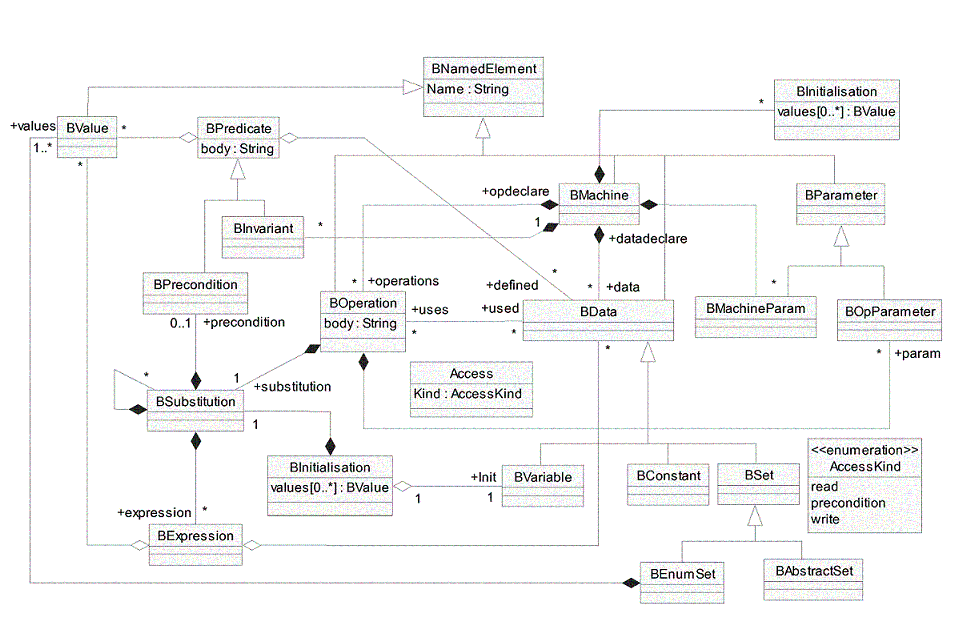metaB1.png
Figure 4: Méta-modèle UML pour la spécification de machines abstraites B

1.2  Spécification de types en B

Nous faisons le choix ici de représenter une syntaxe abstraite issue des constructions les plus couramment utilisées au sein des machines B. En effet, nous n'illustrons pas à un méta-niveau les fondements (ou axiomes) de B. Par exemple, une variable R peut être définie au niveau de l'invariant par :
R = {r | r ∈ \pow(E1 ×E2) ∧∀x, y, z ·(x,y ∈ r ∧x,z ∈ r ⇒ y = z)}
avec E1 et E2 deux ensembles abstraits (instances de BAbstractSet). Cependant, une telle variable est couramment définie par : R ∈ E1 \pfun E2 et correspond à une fonction partielle. Notre méta-modèle convient donc à cette deuxième construction de R. La Fig. 9 présente le méta-modèle complet correspondant aux spécifications de types en B.


BTypedElement.   Regroupe les éléments typés d'une machine abstraite : les paramètres, les constantes, les variables ainsi que les valeurs pré-définies par le langage ou définies par énumération.
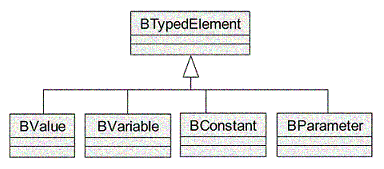BTypedElementMeta.png
Figure 5: Spécialisations de BTypedElement
TypingPredicate (Fig. 6).   Définit les prédicats de typage en B à partir des opérateurs particuliers d'égalité, d'appartenance et d'inclusion. Rappelons que dans la théorie B le typage est simplement réalisé par l'appartenance à un ensemble. Cet ensemble peut être un ensemble de base, ou défini par un constructeur de type ("×","\pow"). Toutefois, étant donné que nous ne représentons pas la théorie B, mais plutôt les notions directement utilisées au sein des machines B, nous faisons la distinction entre les divers opérateurs de typage (la méta-classe TypingOperator). Dans le cadre d'une BValue un prédicat de typage implicite est défini par une appartenance. Un prédicat de typage TypingPredicate est un prédicat B défini par la méta-classe BPredicate. Dans le cadre d'une opération paramétrée le TypingPredicate représente une partie de la BPrecondition associée à la substitution de l'opération en question (voir Fig.  2) et permet de typer les paramètres de l'opération.
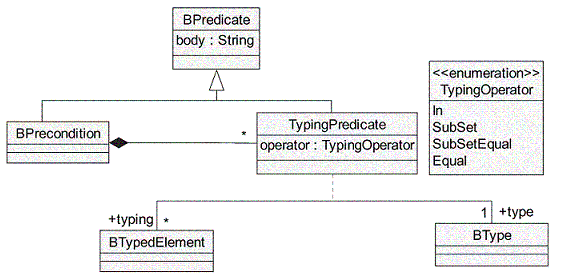BTypedMeta.png
Figure 6: Spécification du mécanisme de typage
BBasicType.   Représente les types de base du langage B. Ces derniers sont constitués des types pré-définis tels que les types BOOL, Z, … mais également des ensembles abstraits et des ensembles énumérés (méta-classe BSet). Les ensembles abstraits sont utilisés pour désigner des objets dont on ne veut pas définir la structure au niveau d'une abstraction. Ils sont alors définis uniquement par leurs noms. Quant aux ensembles énumérés ils sont définis aussi bien par leurs noms que par la liste ordonnée et non vide de leurs éléments énumérés. Les énumérés littéraux d'un ensemble S défini par énumération sont représentés par l'ensemble des instances de la méta-classe BValue liées à l'instance S de la méta-classe BEnumSet. La contrainte de bonne formation de cette classe définit le fait que les éléments d'un BEnumSet S sont typés uniquement par l'ensemble énuméré S.

    (v) Lorsque le BTypedElement d est une BValue, et telle que d est liée par un lien "values" à un BEnumSet S, alors le BType associé à d via un lien TypingPredicate est S.
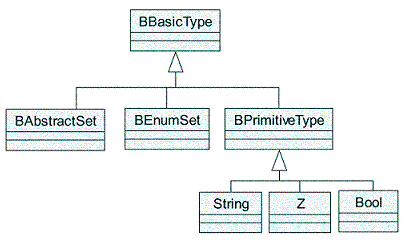BBasicTypeMeta.png
Figure 7: Spécialisations de BBasicType
BComposedType.   Nous désignons par << type composé >> tout type défini à partir d'au moins deux autres types. Il s'agit là précisément de types construits par des expressions de relations fonctionnelles ("\rel","\tfun", etc) ou par un produit cartésien. Chaque BComposedType est donc défini par les BType qui composent son domaine (nom de rôle +dom) et son co-domaine (nom de rôle +ran). Des imbrications de types composés peuvent ainsi être représentées. La méta-classe Multiplicity, est définie particulièrement pour désigner les relations fonctionnelles. Bien que ces multiplicités ne soient pas explicitement définies en B, nous les introduisons au niveau du méta-modèle pour leur adéquation à la transformation de relations B en associations UML. Ces multiplicités sont présentées au niveau du tableau 1 et présentent différentes contraintes d'utilisation établissant le lien entre l'expression utilisée pour définir le type composé et les bornes supérieures et inférieures des multiplicités du domaine et du co-domaine.
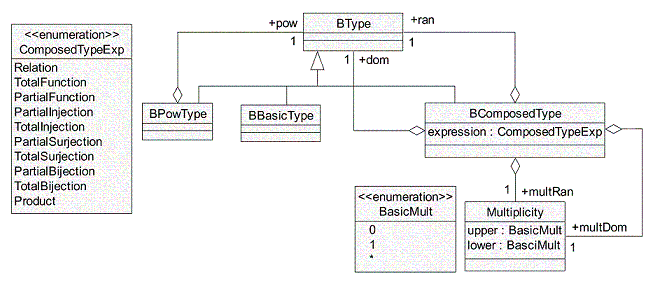BTypeMeta.png
Figure 8: Spécification des types composés
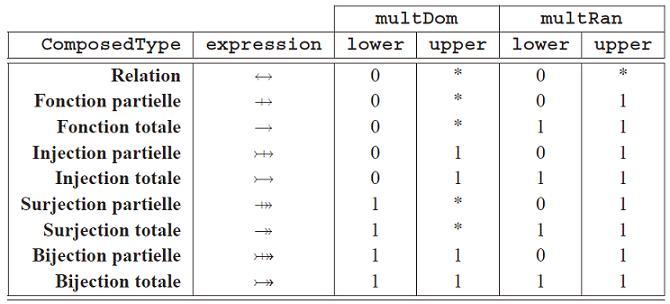mult.jpg
Figure 9: Table des multiplicités associée aux spécialisations de relations fonctionnelles en B
BPowType.   Correspond à un Type construit par le constructeur de type \pow (ensemble des sous-ensembles) appliqué à un BType. Des spécialisations de cette méta-classe peuvent être définies : \pown (ensemble des sous-ensembles non vides), \mathbbF (ensemble des sous-ensembles finis) et \mathbbF1 (ensemble des sous-ensembles finis non vides).

La Fig. 9 présente le méta-modèle proposé pour la spécification des types en B. La distinction entre types de base et types composés nous permettra par la suite de distinguer entre deux familles de schémas de transformation : les transformations de base et les transformation composées. Les transformations de base présentent le niveau de granularité le plus fin car elles sont établies à partir de la spécification des BBasicType, alors que les transformations composées sont établies sur la base de BComposedType et peuvent correspondre à une composition de transformations de base. Notre objectif par là est de distinguer à partir de cette spécification abstraite un ensemble de traductions élémentaires, de telle sorte que toute composition de types peut être traitée. Ainsi, des constructions B complexes peuvent être transformées en UML en les ramenant à des constructions traduisibles par ces traductions élémentaires.
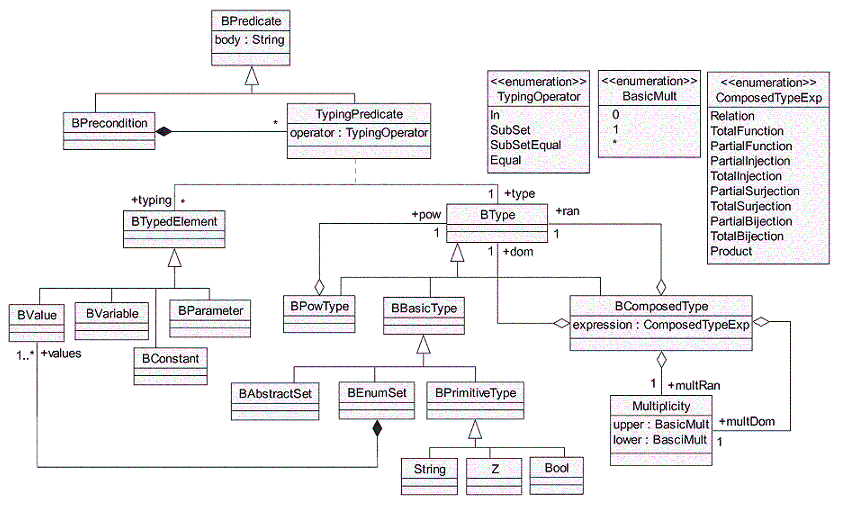metaB2.png
Figure 10: Méta-modèle UML pour la spécification de types en B

1.3  Spécification des structures de raffinement et de composition en B

à ce niveau, nous présentons, uniquement les liens INCLUDES et REFINES entre machines abstraites. La spécification des compositions et des raffinements au niveau du méta-modèle correspondant est plutôt centrée sur les contraintes d'utilisation des méta-classes BMachine, BOperation et BData. Ces contraintes sont des contraintes structurelles définies à partir de la syntaxe abstraite que nous proposons pour B.
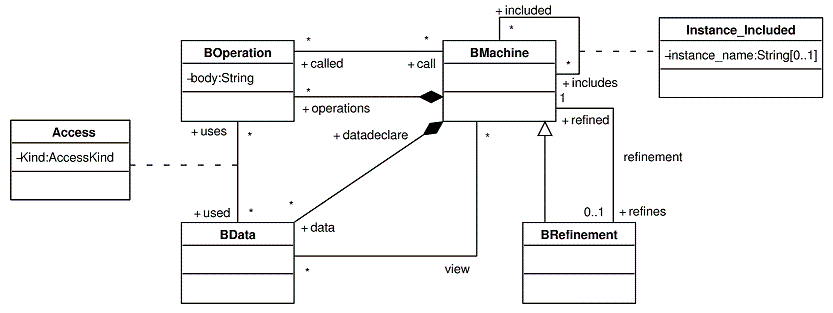MetaB3.png
Figure 11: Spécification des structures de raffinement et de composition en B
Les notions d'invariant de collage, de préservation de cohérence entre raffinements, etc, ne sont pas spécifiées au niveau du méta-modèle. En effet, le méta-modèle que nous proposons présente une vue structurelle des dépendances entre constructions B.

Instance_Included.  Représente l'instance d'une machine abstraite incluse. L'attribut instance_name représente le nom de cette instance. Les noms de rôle +includes et +included sont associés respectivement à la machine incluante et à la machine incluse. Un lien entre une BOperation et une BMachine définissant les rôles +call et +called n'est possible que dans le cas ou un lien Instance entre la BMachine appelant l'opération et la BMachine qui la définit.

    (vi) Une BOperation O peut être appelée (+called) par une BMachine M, si O est déclarée dans une machine M′ et telle que M′ joue le rôle de machine incluse (+included) dans M.

BRefinement.  Illustre un raffinement B sous forme d'une spécialisation de BMachine. En effet, un raffinement peut être vu comme une machine abstraite particulière liée par la clause REFINES à une autre machine abstraite. Les noms de rôle +refines et +refined sont associés respectivement au composant raffinant et au composant raffiné.

    (vii) Une machine abstraite ou un raffinement ne peuvent inclure que des machines abstraites. En effet, un BRefinement ne peut être inclus dans une BMachine.
    (viii) Dans le cas d'un BRefinement, les opérations du raffinement doivent avoir les mêmes noms que celles de la machine raffinée.

Relation view.  Définit un référencement de données d'une BMachine incluse par une BMachine incluante. L'utilisation des données (association "view") est spécifiée par les règles de visibilité. Par exemple, une machine incluante ne peut accéder aux données de la machine incluse qu'en consultation ou via les opérations de la machine incluse. Ces règles sont présentées au niveau de la section  page .

    (ix) Une machine B ne peut référencer des données venant d'autres machines que si un lien d'inclusion ou de raffinement est établi.


Les liens SEES et USES sont similaires au lien d'inclusion et sont naturellement définis par une association réflexive analogue à l'association Instance_Included. Pour ne pas encombrer le diagramme, nous nous sommes limité à la représentation de la clause INCLUDES.

Footnotes:

1 Par invariant nous indiquons aussi bien la clause INVARIANT que la clause PROPERTIES.

Remerciements :

Nous tenons à remercier Laurent Philippe (CEA/Saclay) et Mohamed-Amine Labiadh (LIG/Grenoble) pour leur contribution à l'élaboration du format ecore du méta-modèle.

File translated from TEX by TTH, version 3.86.
On 20 Nov 2009, 11:41.