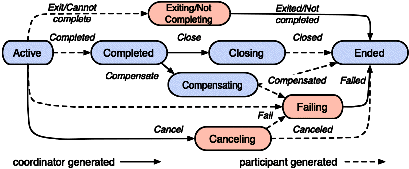
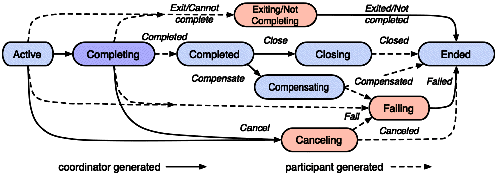
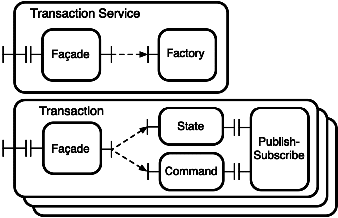
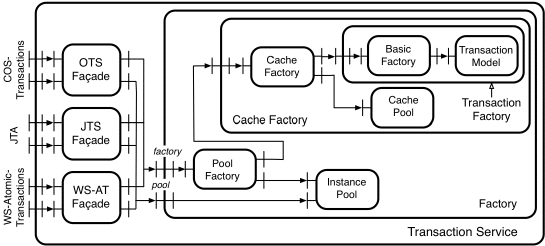
| Transaction T1 | Transaction T2 | ||||
| begin | |||||
| if (A ³ X) | begin | ||||
| {A = A - X} | A = (1+R) A | ||||
| else abort | B = (1+R) B | ||||
| B = B + X | commit | ||||
| commit |
| 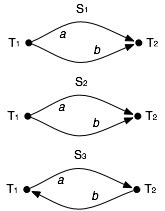 |
Example 1. Consider two transactions T1 and T2, defined as follows:We now have a simple characterization of serializable transactions. A mechanism that allows enforcing serializability is introduced in the next section.A and B denote banking accounts (and the corresponding balances). Transaction T1 transfers an amount X from A to B. Transaction T2 applies an interest rate R to both accounts A and B. In fact, T1 and T2 are patterns for transaction types, in which A, B, X and R are parameters. The integrity constraints are the following: (a) the balance of each account is non-negative; (b) the sum of all accounts is invariant after the execution of a transaction of type T1; and (c) the sum of all accounts involved in a transaction of type T2 is multiplied by (1+R) after the execution of the transaction. Now consider the concurrent execution of two transactions T1 and T2, with parameters a, b, x, r, and assume that, initially, all parameters are positive and a ³ x (so that T1 does not abort). Three possible schedules of this execution are shown below, together with their dependency graphs.
Transaction T1 Transaction T2 begin if (A ³ X) begin {A = A - X} A = (1+R) A else abort B = (1+R) B B = B + X commit commit Schedule S1 is serial (T1; T2). S2 derives from S1 by exchanging two write operations on different objects; since this does not cause a new conflict, S2 is equivalent to S1 and thus is serializable. S3 has a write-write conflict causing the first write on b to be lost, violating consistency. The dependency graph of S3 contains a cycle.
Schedule S1 Schedule S2 Schedule S3 begin1 begin1 begin1 a=a-x a=a-x a=a-x b=b+x begin2 begin2 commit1 a=(1+r)a a=(1+r)a begin2 b=b+x b=(1+r)b a=(1+r)a commit1 commit2 b=(1+r)b b=(1+r)b b=b+x commit2 commit2 commit1
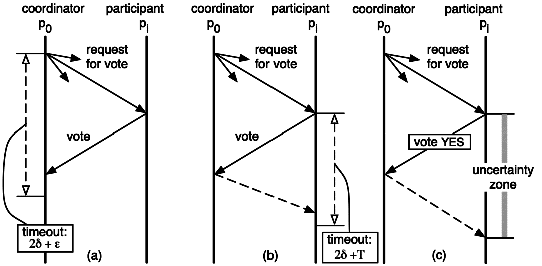
After a transaction has released a lock, it may not obtain any additional locks.A transaction that follows this rule therefore has two successive phases: in the first phase (growing), it acquires locks; in the second phase (shrinking), it releases locks. The point preceding the release of the first lock is called the maximum locking point. The usefulness of 2PL derives from the following result [Eswaran et al. 1976].
Any legal schedule S of the execution of a set {Ti} of well-formed 2PL transactions is conflict-equivalent to a serial schedule. The order of the transactions in this serial schedule is that of their maximum locking points in S.Conversely, if some transactions of {Ti} are not well formed or 2PL, the concurrent execution of {Ti} may produce schedules that are not conflict-equivalent to any serial schedule (and may thus violate consistency).
Example 2. Consider again the two transactions T1 and T2 of Example 1. Here are two possible implementations of T1 (T1a and T1b), and one implementation of T2, using locks (for simplicity, we have omitted the test on the condition x £ a, assuming the condition to be always true).There are two variants of two-phase locking. In non-strict 2PL, a lock on an object is released as soon as possible, i.e., when it is no longer needed. In strict 2PL, all locks are released at the end of the transaction, i.e., after commit. The motivation for non-strict 2PL is to make the objects available to other transactions as soon as possible, and thus to increase parallelism. However, a transaction may abort or fail before having released all its locks. In that case, an uncommitted value may have been read by another transaction, thus compromising isolation, unless the second transaction aborts. Strict 2PL eliminates such situations, and makes recovery easier after a failure (see 9.3.2). In practice, the vast majority of systems use strict 2PL.T1b and T2 are 2PL, while T1a is not. Here are two possible (legal) schedules Sa and Sb, respectively generated by the concurrent execution of T1a, T2 and T1b, T2.
Transaction T1a Transaction T1b Transaction T2 begin1a begin1b begin2 lock_exclusive1a(a) lock_exclusive1b(a) lock_exclusive2(a) a=a-x a=a-x a=(1+r)a unlock1a(a) lock_exclusive1b(b) lock_exclusive2(b) lock_exclusive1a(b) unlock1b(a) b=(1+r)b b=b+x b=b+x unlock2(b) unlock1a(b) unlock1b(b) unlock2(a) commit1a commit1b commit2 Schedule Sa violates consistency, since T2 operates on an inconsistent value of b. Schedule Sb is equivalent to the serial schedule T1b; T2
Sa(T1a, T2) Sb(T1b, T2) begin1a begin1b lock_exclusive1a(a) lock_exclusive1b(a) a=a-x a=a-x unlock1a(a) lock_exclusive1b(b) begin2 unlock1b(a) lock_exclusive2(a) begin2 a=(1+r)a lock_exclusive2(a) lock_exclusive2(b) a=(1+r)a b=(1+r)b b=b+x unlock2(b) unlock1b(b) lock_exclusive1a(b) lock_exclusive2(b) b=b+x b=(1+r)b unlock2(a) commit1b commit2 unlock2(b) unlock1a(b) unlock2(a) commit1a commit2

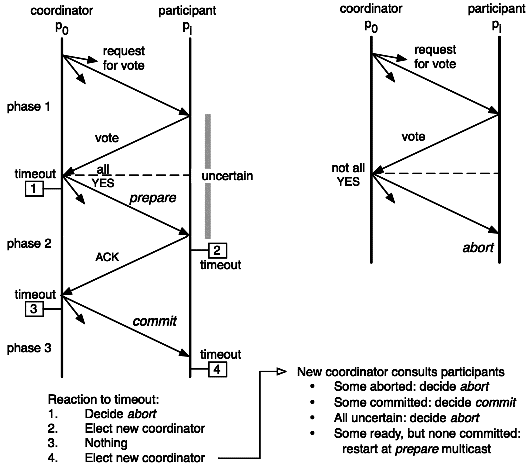
| Commit | Messages | Forced log writes | ||
| protocol | Commit | Abort | Commit | Abort |
| 2PC | 4p | 1+2p | ||
| 2PC-PA | 4p | 3p | 1+2p | p |
| 2PC-PC | 3p | 4p | 2+p | 1+2p |
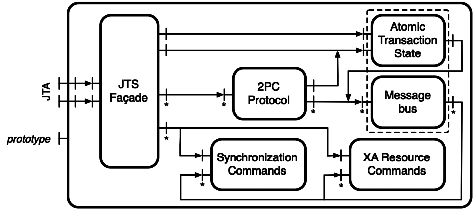
|
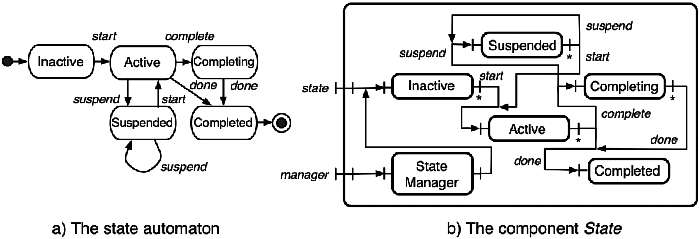
|
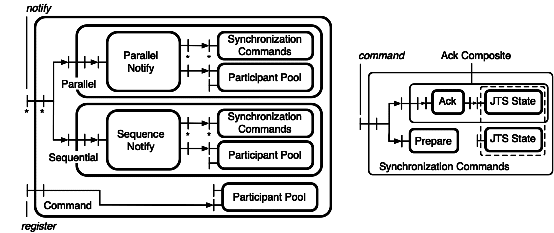
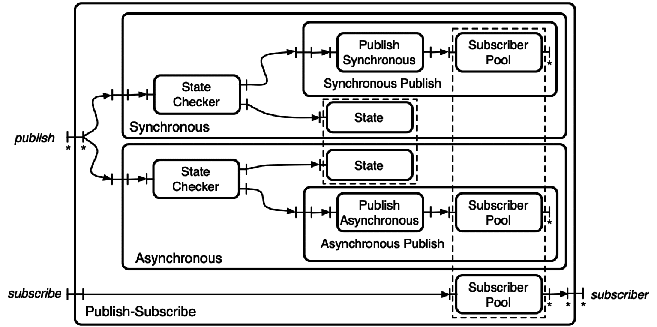
|
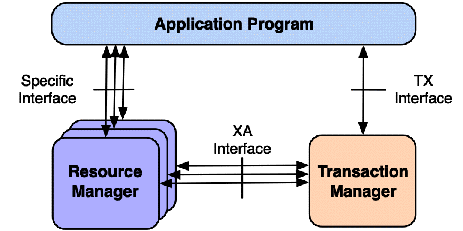
| Transaction attribute | Calling activity | Method's transaction |
| Required | None | T2 |
| T1 | T1 | |
| RequiresNew | None | T2 |
| T1 | T2 | |
| Mandatory | None | Error |
| T1 | T1 | |
| NotSupported | None | None |
| T1 | None | |
| Supports | None | None |
| T1 | T1 | |
| Never | None | None |
| T1 | Error |